A. Pengertian Persamaan Kuadrat

Tujuan Pembelajaran
  1. Siswa mampu mendeskripsikan bentuk umum persamaan kuadrat.

  2. Siswa mampu membedakan mana penyelesaian dan bukan penyelesaian persamaan kuadrat.

  3. Siswa mampu mengidentifikasian yang mana konstanta, variabel, dan koefisien dalam bentuk umum persamaan kuadrat.

      Dalam kehidupan sehari-hari, tanpa kita sadari kita sudah mengenal dan menggunakan persamaan kuadrat. Contohnya, kalian pasti pernah bukan bermain bola basket? Bola basket yang dilemparkan ke dalam ring akan dibuat melambung agar dapat masuk ke dalamnya. Gerakan bola yang melambung ke dalam ring merupakan contoh gambaran persamaan kuadrat.

      Persamaan kuadrat merupakan salah satu persamaan matematika dari variabel yang mempunyai pangkat tertinggi dua, dengan x merupakan variabel, a, b, merupakan koefisien, dan c merupakan konstanta.

1. Bentuk umum

      Bentuk umum persamaan kuadrat dalam x adalah sebagai berikut.

ax2+bx+c=0, dengan a ≠ 0

    Keterangan :
  1. \[x\] sebagai \[variabel\]

  2. \[a\] sebagai \[koefisien\] \[x^2\]

  3. \[b\] sebagai \[koefisien\] \[x\]

  4. \[c\] sebagai \[konstanta\]



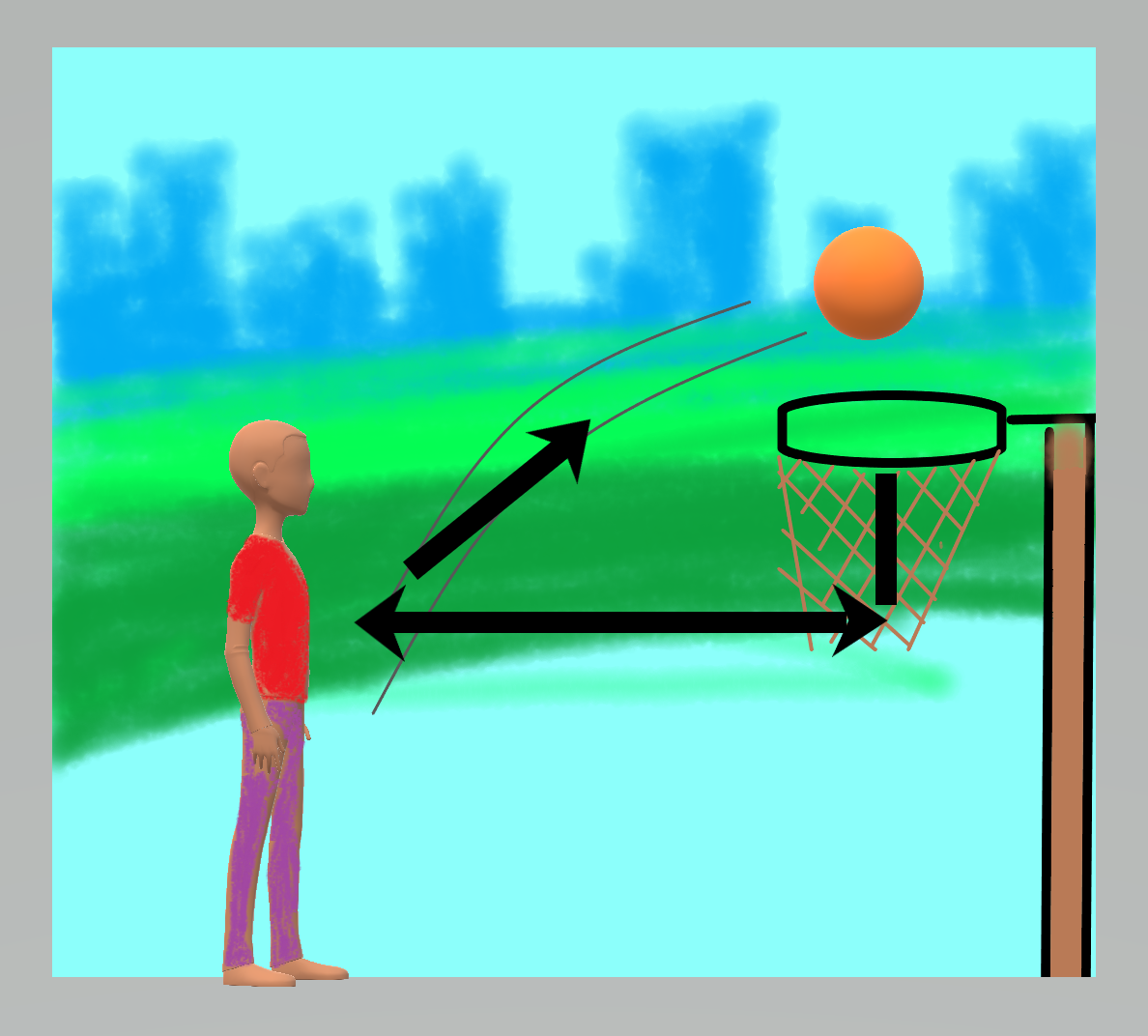
Gambar 1.1

      Gambar di atas memperlihatkan seorang anak yang sedang melempar bola basket ke dalam ring, dapat kita pelajari saat memperkiraan bola yang akan masuk ke dalam ring tersebut adalah contoh penerapan persamaan kuadrat dalam kehidupan sehari-hari. Yakni dari melambungkan bola basket ke dalam ring tersebut diperoleh persamaan kuadrat 2x2 -3x + 1 = 0


Bagaimana cara menentukan nilai a,b, dan c dari persamaan kuadrat 2x2 -3x + 1 = 0 saat bola akan dilambungkan kedalam ring?


Langkah 1

Wajib mengingat ini :

a = koefisien x 2
b = koefisien x
c = konstanta
x = variable

Langkah 2

Menyesuaikan :

      2x2 - 3x + 1 = 0

a        b        c

Dikarenakan a merupakan koefisien dari x2, kemudian b adalah koefisien dari x, dan c adalah konstanta maka, nilai a, b, dan c dari persamaan 2x2 - 3x + 1 = 0 adalah a = 2, b = -3, dan c = 1

Variabel adalah lambang pengganti suatu bilangan yang belum diketahui nilainya dengan jelas.
Contoh:
Suatu biangan jika dikalikan 5 kemudian dikurangi 3, hasilnya adalah 12. Buatlah bentuk persamaannya!
Jawab:
Misalkan bilangan tersebut x berarti 5x-3=12, maka x merupakan variabel.

Koefisien adalah bilangan pada bentuk aljabar yang mengandung variabel.
Contoh:
Tentukan koefisien pada bentuk aljabar berikut.
a. 5x + 3x -1 b. 2x - 1
Jawab:
a. Koefisien dari 5x + 3x -1 adalah 5 dan 3
b. Koefisien dari 2x - 1 adalah 2

Konstanta adalah suku dari suatu bentuk aljabar yang berupa bilangan dan tidak memuat variabel atau bisa dikatakan dia hanya berdiri sendiri tanpa variabel.
Contoh:
Tentukan konstanta pada bentuk aljabar berikut.
a. 2x + 3xy + 5x - y - 4
b. 3 + 7y - x
Jawab:
a. Konstanta adalah suku yang tidak memuat variabel, maka konstanta dari 2x + 3xy + 5x - y - 4 adalah -4
b. Konstanta adalah suku yang tidak memuat variabel, maka konstanta dari 3 + 7y - x adalah 3




Cara menjawab soal :
  1. Tarik angka yang telah disediakan kedalam kolom jawaban.

  2. Klik tombol "Cek Jawaban" untuk mengetahui jawaban tersebut benar atau salah .

  3. Jawaban yang benar akan tepat pada posisinya dan jawaban yang salah akan kembali ke dalam urutan angka yang telah disediakan.

  4. Klik tombol "Ulang" jika ingin mengulangi menjawab soal.

Tentukan nilai a, b, dan c dari setiap persamaan kuadrat berikut ini.

Tentukan nilai a, b, dan c dari setiap persamaan kuadrat berikut ini.

Tentukan nilai a, b, dan c dari setiap persamaan kuadrat berikut ini.





























Nomor Soal:
1 2 3 4 5




*Klik tombol Selanjutnya di bawah ini untuk melanjutkan materi